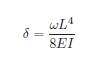How much bigger will wind turbines get?

San Gorgonio Pass Wind Farm. Photo by Chuck Coker.

Wind turbines are large and continue to grow in size. The largest wind turbines now feature towers exceeding 150 meters in height, with blades stretching well over 100 meters. But how large can they become? And how large will they become?

Are There Limits to Wind Turbine Size?

During my time in Denmark working for a wind turbine manufacturer, I attended numerous work anniversaries where the celebrated employee would often give a speech. A common theme emerged in these speeches, typically reflecting on the past:

“When I started here in 1995, wind turbines had 12-meter-long blades, which seemed quite long. We debated their maximum length, settling on around 20 meters as the limit."

And everyone would laugh because by now wind turbine blades are over 100 m long and still growing. So, I wonder, how much longer can they get? In 25 years will today’s graduate engineers be laughing at our 100m blades because by then they’re a kilometre long? That would be over a gigawatt sized wind turbine, it sounds ridiculous. But it sounds equally ridiculous to imagine that after 3 decades of fairly constant growth, that at some point it would just stop.

Will there be 1 GW wind turbines in the future?

A useful way to look at this issue is to start by asking two questions:

Why have wind turbines become as large as they are?
What's preventing them from growing even larger?

Larger wind turbines generate more power and require fewer electrical connections. They are often simpler and less expensive to install and maintain. For instance, managing a wind farm with ten 5MW turbines is more efficient than one with fifty 1MW turbines. Additionally, as turbines increase in size, so do hub heights. Due to wind shear—a phenomenon where wind speeds increase with elevation—larger turbines can access superior wind resources.

Factors in favour of big vs. small wind turbines

However, a larger wind turbine necessitates longer blades, a bigger generator, a more substantial foundation, and likely a taller tower. For many of these components, structural design considerations favour smaller sizes. This preference is best explained by the "square-cube law": As an object's size multiplies, its surface area increases by the square of the multiplier, while its volume—and often its mass and cost—increases by the cube. In summary, larger wind turbines mean more power with fewer machines, while smaller turbines require less material overall.

Aerodynamic efficiency

In the realm of harnessing wind energy and converting it to electricity, which is more aerodynamically efficient - larger or smaller turbines?

Disappointingly, the answer to this question is not as straightforward as one might hope. The reality is that there's no significant scaling effect in terms of aerodynamic efficiency. The maximum amount of energy that a horizontal axis wind turbine can extract from the wind is about 59%, a figure that intriguingly remains consistent regardless of the turbine's size. However, it's not entirely accurate to state that scale has no impact whatsoever on aerodynamic efficiency. While there are some indirect influences related to scale changes, none of these impacts are particularly significant.

This brings us to a tug-of-war between two perspectives: On one side, there are factors that advocate for the continuous enlargement of wind turbines; on the other, reasons that support maintaining smaller sizes. Let's think of these as 'Team Big' and 'Team Small'.

The most expensive turbine components are the rotor, tower and drivetrain assembly.

Our focus will be on the primary components of this debate. We will delve into the most expensive turbine components - the rotor, tower, and drivetrain assembly - as well as significant non-turbine expenses, which include operation, maintenance, and balance of system costs. The latter encompasses all requirements of a wind farm beyond the turbines themselves.

What’s on Team Big and Team Small, and who’s going to win?

There are elements whose costs escalate in direct proportion to power increases. The net effect is a balancing act, where the increase in size doesn't substantially impact the cost of energy from these components. Think of these elements as the audience of the tug-of-war; they're present and essential, but they don't drastically influence the outcome. Let’s call them the audience of this tug of war. Key components in this category include the generator, nacelle, grid connection, and electronics.

Team Big

At the heart of 'Team Big' are the factors previously mentioned. Larger wind turbines have the advantage of accessing faster winds at higher altitudes. They have larger area, enabling them to generate more power. They have fewer electrical connections, require less maintenance visits and are simpler to install if you can get cranes and ships big enough to install them. The cost of everything on team big increases more slowly than power output as turbines get bigger, which help make cheaper energy as wind turbines get bigger.

Interestingly, many components, essential yet standard in every turbine, do not significantly increase in cost with size. A prime example is the turbine controller. This characteristic means that as turbines grow larger, the cost of everything under 'Team Big' scales up more slowly than the power output, contributing to the reduction in energy costs.

Team Small

Shifting our focus to 'Team Small' reveals a more complex scenario. This group comprises components for which costs escalate more rapidly than the power output as turbines increase in size. The primary components under this category include the blades, the tower, and the gearbox and main bearings. To see why, let’s learn a little bit about structural design. Classical beam theory specifically. Wind turbine blades and towers can be conceptualized as cantilever beams. This means one end of these components is fixed, while the other end is free.

Stress

The formula below describes the stress at the support of a cantilever beam with a concentrated load at its tip. Stress (σ) is force (F) divided by area (Lr) , and if you want your structure to not break, you need to keep the maximum stress below the breaking point, the yield stress, of the material you’re using.

I is the area moment of inertia, which is a geometric property that indicates resistance to deflection.

Maximum stress needs to be below the breaking point also known as the yield stress.

For a tubular section, I is calculated using this formula:

Now let’s see what happens if we double all the dimensions of our tubular wind turbine.

Doubling the blade length means quadrupling the power and all the aerodynamic forces along with it. But because we increased the diameter of the tube and its thickness, the maximum stress σ stays the same.

Stiffness

Now on to stiffness, which is also an important constraint for wind turbine blades and towers.

This equation describes the deflection of a tubular beam with a concentrated load at its tip.

E is the modulus of elasticity, which is a property of the material used to make the beam, the stiffness of the material essentially.

The deflection of a twice-as-big tower or blade is twice as large. But obviously so is its length, so its proportional deflection is the same. Therefore, stress and deflection both stay the same as length is increased.

The mass, however, increases by more than the power as blades get longer. We multiplied our lengths by two and we got 4 times the power, but 8 times the mass. There’s that square-cube law.

Blades bending from self-weight

The final structural consideration we’ll look at is bending from self-weight, which is important for wind turbine blades. On every single rotation, gravity bends a blade one way at the 3 o’clock position and then back the other way at the 9 o’clock position. These are small deflections that cause small stresses compared to operational loads or the bending that occurs during a strong gust of wind. However, bending from self-weight is very important because a blade will bend like that millions of times over its life, and even though it’s more than strong enough to withstand that bending load on occasion, after millions of cycles the blade can break, just like when you bend a paperclip repeatedly back and forth.

Bending due to self weight depends on mass per unit length, omega, according to this formula:

And when we double the scale, we quadruple deflection from self-weight.

As blades lengthen, bending from self-weight becomes a more critical factor in design, leading to observable changes in the structural designs of longer blades to accommodate this issue.

Blades (Team Small)

According to our calculations above, in theory the mass of wind turbine blades and towers should increase with the cube of blade length, whereas power is only increasing with the square. And whilst the square-cube law describes how mass increases relative to power, it’s a common assumption that cost increases roughly in line with mass, since the extra mass comes from extra materials and those materials need to be purchased.

Over the past decades, the increase in mass of wind turbine blades relative to their length has been considerably less than what the cubic law would predict. This is because of improvements in blade design and manufacture, and also some materials improvements like using carbon fibre which has a better stiffness-to-weight ratio than fibreglass. The continuity of the current trend in wind turbine blade development is subject to uncertainty. At some point blade masses and costs seem likely to revert to the cubic scaling law, though there are still plenty of ideas being trialled to keep it up a little longer

Carbon fibre has a better stiffness-to-weight ratio than fibreglass. Source

However, it's important to recognize that lower mass does not always equate to lower cost. In the case of carbon fibre, despite resulting in lighter blades, the material is significantly more expensive than fiberglass. This leads to a situation where the use of carbon fibre results in lighter, yet more costly blades.

A couple of examples of technologies that are being trialled to reduce blade masses include ACT Blade’s sail cloth design, and new internal structures in combination with 3D printing and new materials.

ACT Blade: a tensioned textile covered wind turbine blade (source ACT Blade)

However, there are other limitations to blade length continuing to increase forever. As blades get longer, they also get wider, which means they need higher roofs in factories so they can be turned. A 1.5 MW turbine has a blade length of about 33m metres, and a maximum chord of under 3m. If you scale the same blade geometry up to 117m blade length for a 15MW turbine, you’d have a maximum chord over 9m. That is a very cumbersome dimension to deal with, you need specially built factories and turning equipment. Consequently, the latest designs for these larger blades are being modified to somewhat reduce their width, addressing the manufacturing and handling challenges posed by their considerable size.

Transport issues arise as very long blades can’t get around corners easily and large root diameters or wide blades on their edges can’t fit under bridges. Segmented blades with some onsite assembly can get around this, but not without a cost and mass penalty.

Towers (Team Small)

Towers are also subject to the square cube law, but there’s another major issue that’s a bigger obstacle to further increasing tower heights. Modern wind turbine towers are nearly all made of tubular steel sections that are transported to site and then bolted together. [KI1] [KI2] [KI3] That’s a really fast way to install a tower, but it causes some design limitations, at least for onshore turbines. The diameter of these steel sections is limited by what can feasibly be transported on roads, ideally without necessitating excessive road closures or detours to avoid infrastructure like bridges.

As a result, tower designers are restricted in their ability to increase tower widths proportionally with height. To enhance the strength and stiffness of taller towers under these constraints, the solution often involves increasing the thickness of the steel. This approach, however, leads to a significant increase in the use of steel, escalating costs.

Again, there are ways around this. A company called Nabrawind is developing truss tower structures that can be self-assembled in place from smaller sections. Other experimental approaches include 3D printing the lower portions of towers and in-situ spiral welding, as opposed to transporting prefabricated tubular sections. While these solutions are not yet mainstream, the coming decade is likely to witness a shift in tower design, accommodating these novel approaches to meet the challenges of constructing taller wind turbine towers.

Self-erecting tower makes the installation faster. (Source Nabralift)

Drivetrain

The final components we’re going to talk about on team small is the gearbox. I mentioned earlier that the generator is one of the components I’ve put in the “audience.” Its size increases in line with rated power, so a 10MW turbine’s generator is about twice the size and twice the cost of a 5MW one. Now, you might have expected that the gearbox would be the same. However, the low-speed shaft torque is the relevant factor that determines the gearbox mass, and that increases faster than power as the blade length increases. That’s because power equals torque times rotational speed. And a turbine’s rotational speed usually decreases as blade length increases, so as to keep tip speed fairly constant no matter what the turbine size. That’s important for several reasons including aerodynamic efficiency, aerodynamic noise and leading edge erosion. So as rotational speed decreases, torque has to increase making gearboxes another component whose cost increases faster than power output.

In the final analysis of wind turbine components, the gearbox emerges as an interesting case. While the generator's size and cost scale linearly with the turbine's rated power—evidenced by a 10MW turbine's generator being roughly twice the size and cost of a 5MW turbine's—the gearbox follows a different pattern. The mass of the gearbox is primarily determined by the low-speed shaft torque, which increases faster than the power as blade length increases. This is because power is a function of torque and rotational speed, and the rotational speed of a turbine typically decreases with longer blades to maintain constant tip speed. This constant tip speed is crucial for aerodynamic efficiency, noise reduction, and minimizing leading-edge erosion. Therefore, as the rotational speed decreases and torque increases, gearboxes become a component where the cost escalates more rapidly than the power output.

Rotational speed of the turbine decreases as blade length increases to keep tip speed constant. (Source)

Overall Optimisation

Those are the major features of a wind farm development and how their costs vary with turbine size. Numerous researchers have employed complex algorithms to determine the "optimal" turbine size. However, this optimum is fluid, shifting as technology evolves. The changing size of wind turbines is not a result of an inability to create larger turbines, but rather a reflection of the current state of technology and the associated costs of wind farm development and maintenance. At present, making turbines larger than they currently are would simply be more costly. The "optimal" turbine size at any given moment tends to align closely with what is available on the market. This is because wind turbine manufacturers are highly motivated to design turbines that offer the lowest overall cost of wind energy.

Future Predictions

How will this tug of war play out in the future? To state it very simply, we have structural design factors wanting turbines to stay small, and pretty much everything else favouring wind turbines getting bigger. So far, wind turbines are getting bigger, which means Team Big is winning. This is especially true for offshore wind, where transport constraints aren’t much of a factor because you can build factories right near a port and avoid putting anything big onto trucks.

When I started my PhD research on wind turbine blade structural design back in 2012, I was using a 30m reference blade design, from a 1.5MW turbine. I think the world’s longest blades at that time were around 50m, on 3MW turbines. The current largest onshore turbine is Vestas’ 7.2 MW V172 with 84m long blades, and the largest offshore wind turbines are over 12MW and with blades longer than 108m. This decade has seen blade lengths more than double and power output quadruple.

Current largest onshore wind turbine is Vestas’ 7.2 MW V172. (Source)

Will this trend of increasing size continue indefinitely? By 2032, could we witness another doubling in blade length to 220m and a quadrupling of power to 50MW turbines? While this seems unlikely, caution is advised in setting limits on future growth, as history has shown the tendency to underestimate the potential of wind energy advancements. We may not reach the technological ceiling of how large wind turbines could potentially be built. Technically, constructing a 200m or even a 500m long wind turbine blade on an 800m tower is feasible, but the real issue is whether such undertakings would represent a prudent investment of resources.

Instead, the future likely holds different avenues for reducing the cost of wind energy, moving beyond the paradigm of simply building larger turbines. These technologies might be ways to put turbines in better wind resources. These might include new technologies like floating offshore wind, which might be vertical axis turbines. It might be airborne wind energy, or multirotor designs. Or something else that hasn’t even been thought of yet.

Vestas 900kW four-rotor concept design in Roskilde, Denmark. (source)

Watch this content as a video on Engineering with Rosie on YouTube.